Законы Дэ Моргана

Зако́ны^[1]^[2]^[3], або пра́вілы Дэ Мо́ргана — два правілы пераўтварэньня ў лёгіцы выказваньняў і булевай альгебры, якія зьяўляюцца адначасна і дзейнымі правіламі вывядзеньня. Названыя ў гонар брытанскага матэматыка XIX стагодзьдзя Агастэса Дэ Моргана. Гэтыя правілы дазваляюць выразіць кан’юнкцыю і дыз’юнкцыю адна праз другую з дапамогай адмаўленьня.

Словамі гэтыя правілы можна выразіць так:

Адмаўленьне дыз’юнкцыі ёсьць кан’юнкцыя адмаўленьняў
Адмаўленьне кан’юнкцыі ёсьць дыз’юнкцыя адмаўленьняў

ці

Дапаўненьне аб’яднаньня двух мностваў роўнае перасячэньню іхніх дапаўненьняў
Дапаўненьне перасячэньня двух мностваў роўнае аб’яднаньню іхніх дапаўненьняў

ці

не (A або B) = (ня A) і (ня B)
не (A і B) = (ня A) або (ня B)

дзе «A ці B» ёсьць «інклюзіўным або», то бок прынамсі адзін з A або B, а ня «выключальнае або», якое патрабуе дакладна адно з A або B.

Па сваёй сутнасьці гэтыя законы — гэта сувязь максімума празь мінімум і наадварот. Дыз’юнкцыя грае ролю максімума, кан’юнкцыя — мінімума. Такая сувязь дзейнічае ня толькі ў дыскрэтных прасторах:

$min(a,b)=-max(-a,-b)$ $max(a,b)=-min(-a,-b)$

У тэорыі мностваў і булевай альгебры яны фармальна запісваюцца такім чынам:

{\begin{aligned}{\overline {A\cup B}}&={\overline {A}}\cap {\overline {B}},\\{\overline {A\cap B}}&={\overline {A}}\cup {\overline {B}},\end{aligned}}

дзе

$A$ і $B$ — мноствы,
${\overline {A}}$ — дапаўненьне $A$ ,
$\cap$ — перасячэньне,
$\cup$ — аб’яднаньне.

Законы Дэ Моргана ў запісе фармальнай мовай выглядаюць так:

\neg (P\lor Q)\iff (\neg P)\land (\neg Q),

і

\neg (P\land Q)\iff (\neg P)\lor (\neg Q)

дзе

P і Q — выказваньні,
$\neg$ — апэратар лягічнага адмаўленьня (NOT),
$\land$ — апэратар лягічнай кан’юнкцыі (AND),
$\lor$ — апэратар лягічнай дыз’юнкцыі (OR),
$\iff$ — мэталягічны сымбаль са значэньнем «можа быць заменены ў лягічным доказе на», часта называны папросту «тады і толькі тады». У любым спалучэньні ісьцінных/ілжывых значэньняў P і Q левы і правы бакі стрэлкі пасьля вылічэньняў будуць мець аднолькавыя значэньні ісьціннасьці.

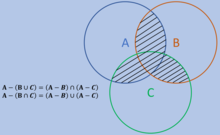
Яшчэ адна форма выражэньня законаў Дэ Моргана прыведзеная на схеме справа.

A-(B\cup C)=(A-B)\cap (A-C),

A-(B\cap C)=(A-B)\cup (A-C).

Правілы Дэ Моргана прымяняюцца дзеля спрашчэньня лягічных выразаў у кампутарных праграмах і распрацоўцы мікрасхемаў. Гэтыя правільны ёсьць прыкладам шырэйшага панятку матэматычнай дуальнасьці.

Мінуўшчына

Законы названыя ў гонар Агастэса Дэ Моргана (1806—1871)^[5], які ўвёў у клясычнае зьлічэньне выказваньняў фармальную вэрсію законаў. Што праўда, яшчэ Арыстотэль правёў падобныя назіраньні, таму старажытным грэкам і сярэднявечным лёгікам яны былі вядомыя^[6]. Прыкладам, у XIV стагодзьдзі Ўільям Окам выразіў правілы словамі на паперы^[7]. Жан Бурыдан у сваёй Summulae de Dialectica таксама апісвае законы перамяненьня, якія адпавядаюць дэморганавым^[8]. Тым ня меней, менавіта Дэ Морган сфармуляваў іх у тэрмінах сучаснай фармальнай лёгікі і паклаў іх на мову лёгікі. Гэтыя фармулёўкі лёгка даказаць, і яны нават выглядаюць трывіяльнымі^[9].

Нефармальны доказ

Дэмораганава тэарэма можа дастасоўвацца да адмаўленьня дыз’юнкцыі або адмаўленьня кан’юнкцыі ва ўсіх частках формулы.

Адмаўленьне дыз’юнкцыі

Дзеля дастасаваньня да дыз’юнкцыі разгледзім такое сьцьверджаньне: «Хлусьня тое, што альбо A, альбо B ісьцінныя» — якое запісваецца так:

\neg (A\lor B).

Такім чынам, паколькі ані A, ані B ня ісьцінныя, адсюль вынікае, што як A ня ісьціннае, так і B ня ісьціннае, што можна запісаць так:

(\neg A)\wedge (\neg B).

Калі б A ці B былі ісьціннымі, тады дыз’юнкцыя а A і B была б ісьціннай, а ейнае адмаўленьне хлусьлівым. Словамі гэта адпавядае лёгіцы «паколькі абодва сьцьверджаньні хлусьлівыя, то хлусьліва і тое, што адно зь іх ісьціннае».

І наадварот, другі выраз сьцьвярджае, што A хлусьлівае і B хлусьлівае (або іначай, «ня A» і «ня B» ісьцінныя). Ведаючы гэта, ведаем, што і дыз’юнкцыя A і B таксама будзе хлусьлівай. А адмаўленьне такой дыз’юнкцыі будзе ісьцінным, што ідэнтычна першаму сьцьверджаньню.

Адмаўленьне кан’юнкцыі

Дастасаваньне тэарэмы Дэ Моргана да кан’юнкцыі падобна дастасаваньню да дыз’юнкцыі як у форме, так і ў доказе. Разгледзім такое сьцьверджаньне: «Хлусьня тое, што A і B абодва ісьцінныя» — якое запісваецца так:

\neg (A\land B).

Каб гэтае сьцверджаньне было ісьцінным, адно з ці абодва A і B мусяць быць хлусьлівымі, бо калі б яны абодва былі ісьціннымі, то кан’юнкцыя A і B была б ісьціннай, тады сьцьверджаньне стала б хлусьлівым. Адсюль (прынамсі) адно ці болей з A і B мусяць быць хлусьлівымі (або іначай, адно ці болей зь «ня A» і «ня B» мусяць быць ісьціннымі). Гэта можна запісаць так:

(\neg A)\lor (\neg B).

Кажучы простай мовай, гэта адпавядае лёгіцы «паколькі сьцьверджаньне пра тое, што абодва сьцьверджаньні ісьцінныя — хлусьлівае, прынамсі адно зь іх мусіць быць хлусьлівым».

І зноўку ў адваротным кірунку, другі выраз сьцьвярджае, што прынамсі адно зь «ня A» і «ня B» мусяць быць ісьціннымі (або іначай, прынамсі адно з A і B мусіць быць хлусьлівым). Паколькі прынамсі адно зь іх хлусьлівае, тады іхняя кан’юнкцыя таксама будзе хлусьлівай. Адмаўленьне такой кан’юнкцыі становіцца ісьцінным, што ідэнтычна першаму сьцьверджаньню.

Глядзіце таксама

Пазытыўная лёгіка
Ізамарфізм — апэратар NOT ёсьць ізамарфізмам між пазытыўнай і нэгатыўнай лёгікай

Крыніцы

^ Irving M. Copi, Carl Cohen, Kenneth McMahon. Introduction to Logic.
^ Hurley, Patrick J. A Concise Introduction to Logic. — 12th. — Cengage Learning, 2015. — ISBN 978-1-285-19654-1
^ Moore, Brooke Noel Critical thinking. — 10th. — New York: McGraw-Hill, 2012. — ISBN 978-0-07-803828-0
^ Kashef, Arman. In Quest of Univeral Logic: A brief overview of formal logic's evolution. — 2023.
^ DeMorgan’s Theorems at mtsu.edu
^ Bocheński’s History of Formal Logic
^ William of Ockham, Summa Logicae, part II, sections 32 and 33.
^ Jean Buridan, Summula de Dialectica. Trans. Gyula Klima. New Haven: Yale University Press, 2001. See especially Treatise 1, Chapter 7, Section 5. ISBN 0-300-08425-0
^ Augustus De Morgan (1806—1871) by Robert H. Orr

Літаратура

Логіка выказванняў: вучэбны дапаможнік / Гарбузаў, Віктар Мікалаевіч; Немец, Уладзімер Сьцяпанавіч; ГрДУ імя Я. Купалы. — Гродна: ГрДУ, 1997. — 44 с.
Матэматыка: вучэб.-мэтад. дапам. У 2 ч. Ч. 1 — 2-е выд., перапрац. / Баранцэвіч, Канстанцін Зянонавіч; Пакала, Аляксандар Анатольевіч. — Мн., БДПУ, 2005. — 176 с.
Матэматыка: вучэб.-мэтад. дапам. У 2 ч. Ч. 1. / Баранцэвіч, Канстанцін Зянонавіч; Пакала, Аляксандар Анатольевіч. — Мн., 1996.
Геаметрыя 7 — 11. / Пагарэлаў А. — Мн., 1991.
Задачнік-практыкум па матэматыцы / Пакала А. А. — Мн., 1994.
Асновы пачатковага курса матэматыкі / Стойлава Л. П., Пышкала А. М.— Мн., 1990.

Вонкавыя спасылкі

Законы Дэ Моргана Матэматычная энцыкляпэдыя. EMS Press (2001).
Weisstein, Eric W. Законы Дэ Моргана MathWorld
Законы Дэ Моргана на PlanetMath.
Дуальнасьць у лёгіцы і мове, Інтэрнэт-энцыкляпэдыя філязофіі.

[1] Irving M. Copi, Carl Cohen, Kenneth McMahon. Introduction to Logic.

[2] Hurley, Patrick J. A Concise Introduction to Logic. — 12th. — Cengage Learning, 2015. — ISBN 978-1-285-19654-1

[3] Moore, Brooke Noel Critical thinking. — 10th. — New York: McGraw-Hill, 2012. — ISBN 978-0-07-803828-0

[Quest_Univeral_Logic-4] Kashef, Arman. In Quest of Univeral Logic: A brief overview of formal logic's evolution. — 2023.

[5] DeMorgan’s Theorems at mtsu.edu

[6] Bocheński’s History of Formal Logic

[7] William of Ockham, Summa Logicae, part II, sections 32 and 33.

[8] Jean Buridan, Summula de Dialectica. Trans. Gyula Klima. New Haven: Yale University Press, 2001. See especially Treatise 1, Chapter 7, Section 5. ISBN 0-300-08425-0

[9] Augustus De Morgan (1806—1871) by Robert H. Orr

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]