Тэарэма Мэнэлая
Тэарэ́ма Мэнэла́я — гэта клясычная тэарэма афіннай геамэтрыі.
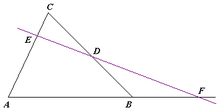

Калі пункты і ляжаць адпаведна на прамых і трохкутніка , то яны калінэарныя, але толькі тады, калі
Тут , і азначаюць адносіны накіраваных адрэзкаў. У прыватнасьці, з тэарэмы вынікаюць суадносіны для даўжынь:
Гісторыя
рэдагавацьПадобны вынік у сфэрычнай геамэтрыі сустракаецца ў трактаце «Sphaerica» Мэнэлая Александрыйскага (прыблізна 100-ы год нашай эры) і хутчэй за ўсё, аналягічны вынік на плоскасьці быў ужо вядомы. Гэтая тэарэма носіць імя Мэнэлая, бо ранейшых пісьмовых успамінаў аб гэтым выніку не захавалася.
Доказ
рэдагавацьПравядзем праз пункт С прамую, паралельную прамой AB, і абазначым цераз K пункт перасячэньня гэтай прамой з прамой DF. Трохкутнікі і падобныя (па двум вуглам), таму
і, значыць —
- .
З другога боку, падобнымі зьяўляюцца таксама і трохкутнікі і , таму
і, такім чынам —
- .
Але ў такім выпадку
або
- .
Магчымыя два разьмяшчэньні пунктаў і , альбо два зь іх ляжаць на адпаведных баках трохкутніка і адзін на падаўжэньні, альбо ўсе тры ляжаць на падаўжэньнях адпаведных бакоў, адсюль для адносін накіраваных адрэзкаў маем









